Fonctions du Troisième Degré
Ici, vous trouverez des exercices pour vous entraîner sur les fonctions du troisième degré, un outil essentiel en analyse mathématique.
Revoyons ensemble les points essentiels sur les fonctions du troisième degré avant de démarrer les exercices. Ces rappels sont vos fondations pour réussir !
1. Forme générale d'une fonction du troisième degré
Une fonction du troisième degré, ou fonction cubique, est une fonction polynomiale de degré 3. Sa forme générale est donnée par :
$$f(x) = ax^3 + bx^2 + cx + d$$où $a$, $b$, $c$, et $d$ sont des coefficients réels, et $a \neq 0$. Dans les exercices qui suivent, nous nous concentrerons principalement sur des formes simplifiées comme $f(x) = ax^3$ et $f(x) = ax^3 + b$.
2. Sens de variation des fonctions $x \mapsto ax^3$ et $x \mapsto ax^3 + b$
Le sens de variation de ces fonctions dépend du signe du coefficient $a$.
Si $a > 0$ : La fonction $f(x) = ax^3$ (et aussi $f(x) = ax^3 + b$) est strictement croissante sur $\mathbb{R}$.
Si $a < 0$ : La fonction $f(x) = ax^3$ (et aussi $f(x) = ax^3 + b$) est strictement décroissante sur $\mathbb{R}$.
La constante $b$ dans $f(x) = ax^3 + b$ provoque une translation verticale du graphe de $f(x) = ax^3$, mais ne modifie pas le sens de variation.
3. Racines d'une fonction polynôme de degré 3
Une fonction polynôme de degré 3 peut avoir une, deux ou trois racines réelles. Dans la forme factorisée $f(x) = a(x - x_1)(x - x_2)(x - x_3)$, les racines sont directement $x_1$, $x_2$, et $x_3$.
Pour trouver les racines d'une forme non factorisée, on peut parfois factoriser ou utiliser des méthodes numériques ou graphiques.
4. Transformations graphiques
Translation verticale : Ajouter une constante $b$ à $f(x)$ (passer de $f(x)$ à $f(x) + b$) translate le graphe verticalement de $b$ unités vers le haut si $b>0$ et vers le bas si $b<0$.
Dilatation/Compression verticale : Multiplier $f(x)$ par une constante $a$ (passer de $f(x)$ à $a \cdot f(x)$) étire ou compresse le graphe verticalement. Si $|a| > 1$, c'est une dilatation ; si $0 < |a| < 1$, c'est une compression ; si $a < 0$, il y a aussi une réflexion par rapport à l'axe des x.
C'est noté ? 💪 Maintenant, place aux exercices ! Bonne chance !
Exercice 1
Donner le sens de variation de chacune des fonctions définies sur $\mathbb{R}$:
- $f(x) = -6x^3$
- $f(x) = -2,5x^3$
Exercice 2
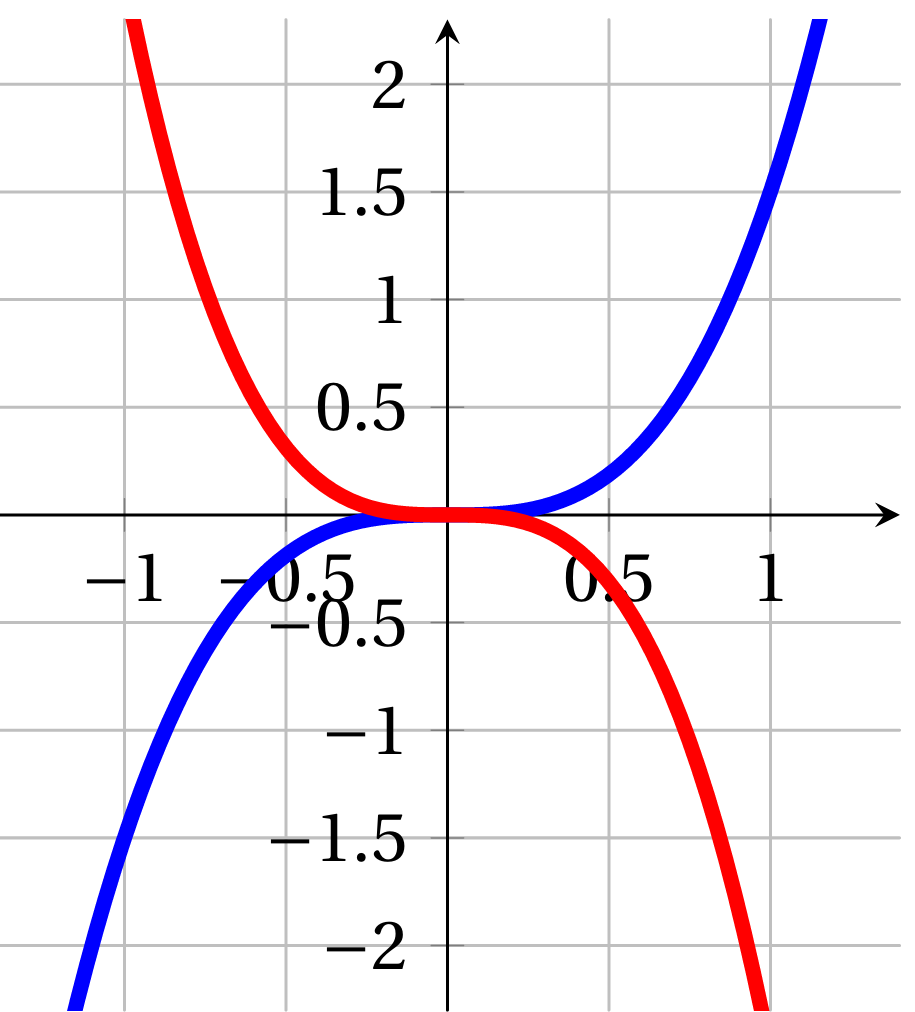
Relier chacune des fonctions définies sur $\mathbb{R}$ suivantes à la courbe correspondante. Justifier. $$g(x) = 1,5x^3 \quad \text{et} \quad i(x) = -2,5x^3$$
Exercice 3
Soit $h$ la fonction définie sur $\mathbb{R}$ par $h(x) = ax^3$. Déterminer la valeur de $a$ sachant que $h(4) = 32$.
Exercice 4
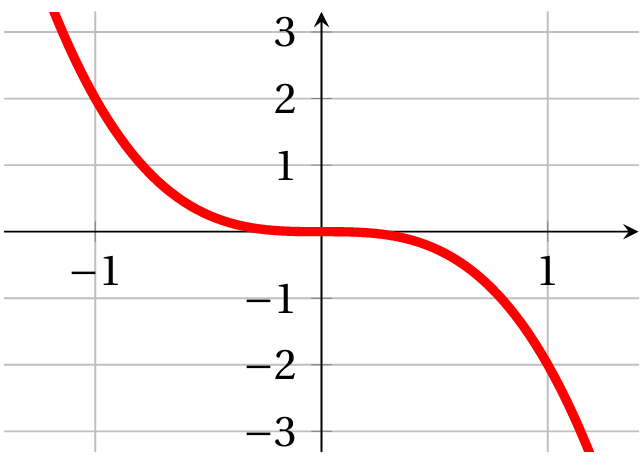
On a représenté la fonction $g$ définie sur $\mathbb{R}$ par $g(x) = ax^3$ sur une calculatrice. Déterminer l'expression de la fonction ainsi représentée.
Exercice 5
On donne le tableau de valeurs d'une fonction du type $x \mapsto ax^3$. Déterminer la valeur de $a$.
| $x$ | -4 | -3 | -2 | -1 | 0 | 1 | 2 |
|---|---|---|---|---|---|---|---|
| $f(x)$ | 192 | 81 | 24 | 3 | 0 | -3 | -24 |
Exercice 6
Donner le sens de variation de chacune des fonctions définies sur $\mathbb{R}$:
- $f(x) = -5x^3 - 4$
- $f(x) = -3x^3 + 6$
Exercice 7
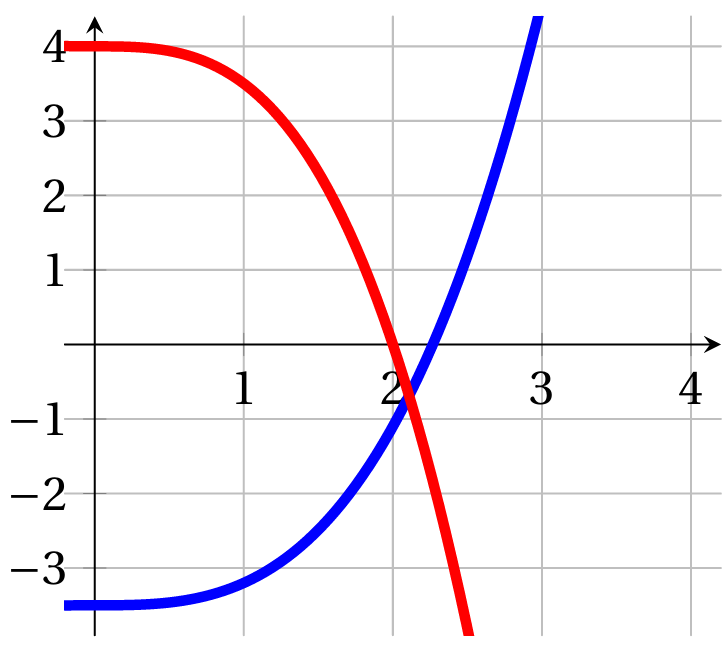
Relier chacune des fonctions définies sur $\mathbb{R}$ suivantes à la courbe correspondante. Justifier. $$f(x) = 0,3x^3 - 3,5 \quad \text{et} \quad h(x) = -0,5x^3 + 4$$
Exercice 8
Soit $f$ la fonction définie sur $\mathbb{R}$ par $f(t) = at^3 + b$. Déterminer la valeur de $a$ et de $b$ sachant que $f(-1) = -3$ et $f(2) = 15$.
Exercice 9
On a représenté la fonction $g$ définie sur $\mathbb{R}$ par $g(x) = ax^3 + b$ sur une calculatrice. Déterminer l'expression de la fonction ainsi représentée.
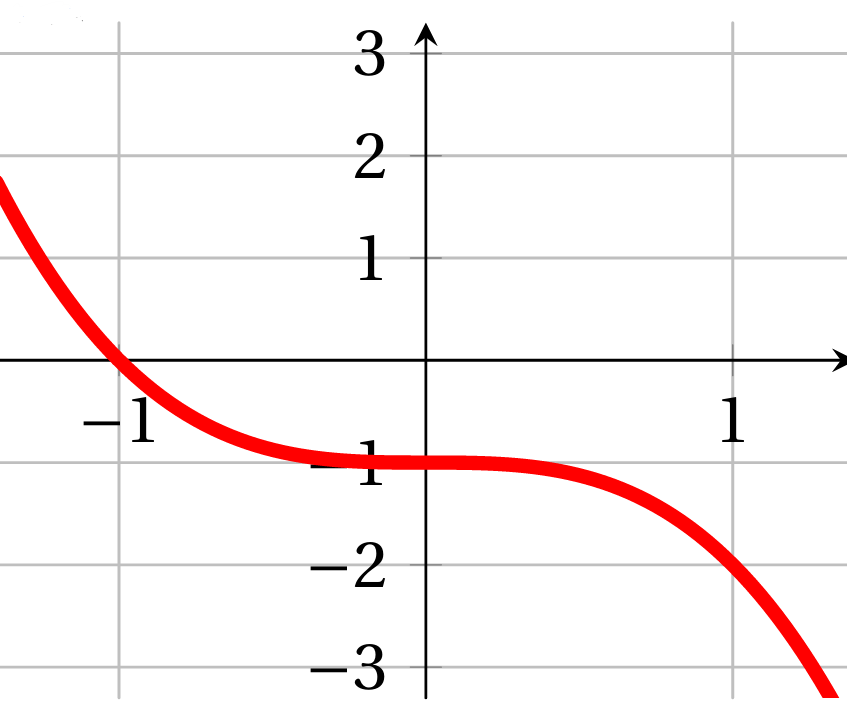
Exercice 10
On donne le tableau de valeurs d'une fonction du type $x \mapsto ax^3 + b$. Déterminer la valeur de $a$ et $b$.
| $x$ | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|---|---|---|
| $f(x)$ | 55 | 17 | 3 | 1 | -1 | -15 | -53 | -127 | -249 |
Exercice 11
Indiquer quelle transformation permet de passer de la courbe représentative de la fonction $f$ à celle de la fonction $g$.
- $f$ et $g$ sont définies sur $[-3;3]$ par $f(x) = -2,3x^3$ et $g(x) = -2,3x^3 - 3,2$.
- $f$ et $g$ sont définies sur $[-5;5]$ par $f(x) = 53x^3$ et $g(x) = -53x^3 - 64$.
Exercice 12
Donner les racines des fonctions polynômes de degré 3 suivantes :
- $f(x) = 2(x-3)(x+5)(x+2)$
- $g(t) = -4(t-3,2)\left(t-\dfrac{2}{3}\right)(t+1)$
Exercice 13
Déterminer algébriquement les racines de la fonction $f$ définie sur $\mathbb{R}$ par $f(x) = x^3 - 8$.
Exercice 14
Déterminer l'expression de la fonction polynôme $f$ de degré 3 définie sur $\mathbb{R}$ sachant qu'elle admet trois racines : $1$, $(-2)$ et $4$ et que $f(0) = 16$.
Exercice 15
Déterminer, l'expression de la fonction polynôme de degré 3 en vous appuyant sur sa représentation graphique. On admettra que 2 est racine double et -1 racine simple.
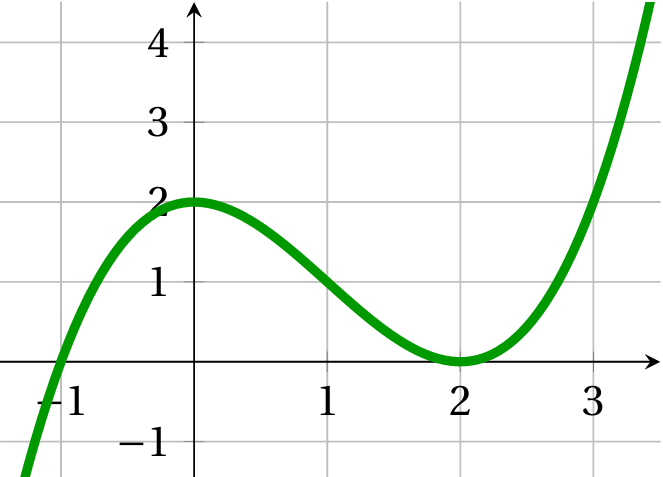
Exercice 16
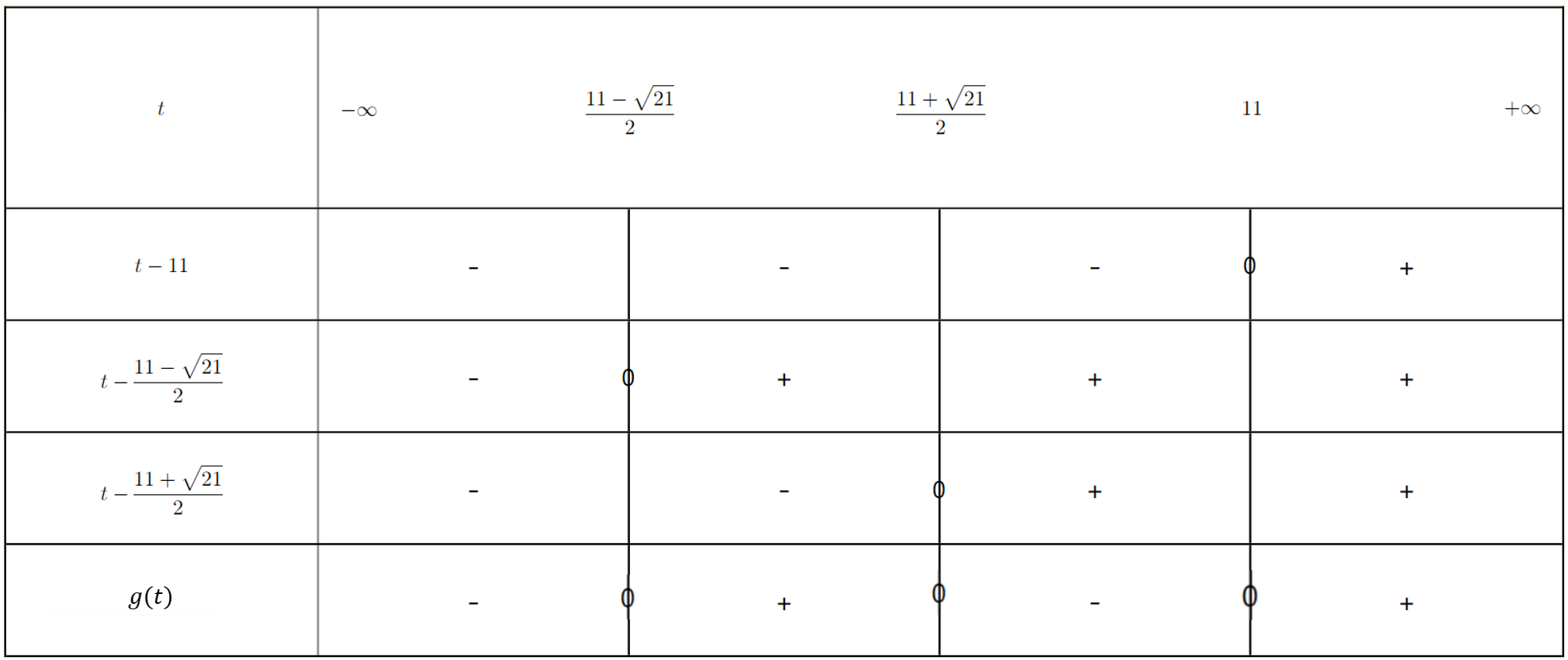
Partie A : Étude graphique
La courbe donnée ci-contre représente la concentration en mg.L$^{-1}$ du produit actif dans le sang du malade en fonction du temps écoulé depuis l'injection du médicament.
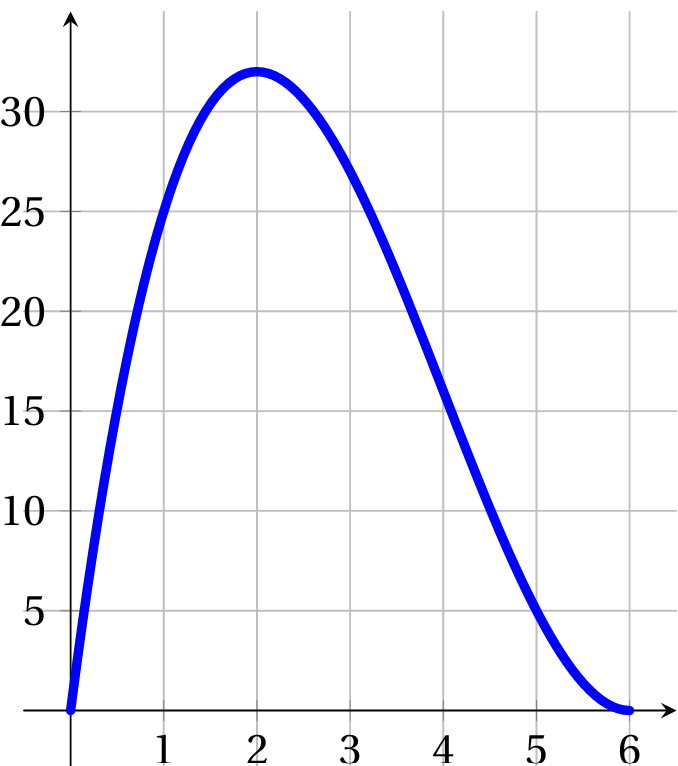
- Déterminer la concentration en mg.L$^{-1}$ du produit actif pour $t = 5$.
- Le médecin a-t-il respecté la dose à ne pas dépasser ? Expliquer.
- Déterminer les temps en heures et minutes pour lesquels la quantité de produit actif est de $15$mg.L$^{-1}$.
- Quelle est la durée pendant laquelle le médicament est resté efficace ?
- Au bout de quelle durée le médicament est-il complètement éliminé ?
On admet que la concentration, exprimée en mg.L$^{-1}$, du produit actif dans le sang du malade est donnée en fonction du temps $t$, exprimé en heures, par la fonction $f$ définie sur l'intervalle $[0;6]$ par : $f(t) = t^3 - 12t^2 + 36t$. On cherche sur quel intervalle de temps la concentration du produit actif est supérieure ou égale à $25$mg.L$^{-1}$. Pour cela, on définit la fonction $g$ sur $[0;6]$ par $g(t) = f(t) - 25$.
- Reproduire et compléter le tableau suivant :
$t$ $0$ $1$ $2$ $3$ $4$ $5$ $6$ $g(t)$ $-25$ $0$ $3$ $2$ $-1$ $0$ $11$ - A l'aide de la fonction TABLE de calculatrice ou d'un logiciel de tableur, déterminer une valeur approchée au dixième près des racines du polynôme $t^3 - 12t^2 + 36t - 25$.
- Vérifier que $g(t) = (t-1)\left(t-\dfrac{11-\sqrt{21}}{2}\right)\left(t-\dfrac{11+\sqrt{21}}{2}\right)$.
- Étudier le signe de la fonction $g$.
- En déduire l'intervalle de temps pendant lequel le médicament est efficace.